
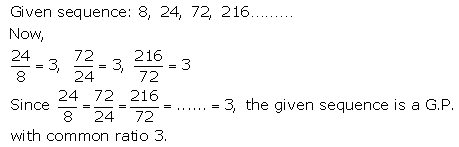
Proof of Sum of Infinite Geometric Progression FormulaĬonsider an infinite geometric sequence a, ar, ar 2. and the sum of the first n terms, in this case, S n = a + a + a +. If r = 1, the progression looks like a, a, a. Since (r - 1) is in its denominator, it is defined only when r ≠ 1. Subtracting equation (1) from equation (2), Proof of Sum of Finite Geometric Progression FormulaĬonsider a finite geometric progression of n terms, a, ar, ar 2.
Geometric sequence examples with solutions series#
If the number of terms in a geometric progression is infinite, then the sum of the geometric series is calculated by the formula: If the number of terms in a geometric progression is finite, then the sum of the geometric series is calculated by the formula: As we read in the above section that geometric progression is of two types, finite and infinite geometric progressions, hence the sum of their terms is also calculated by different formulas.

The geometric progression sum formula is used to find the sum of all the terms in a geometric progression. is an infinite series where the last term is not defined. It is the progression where the last term is not defined. Infinite geometric progression contains an infinite number of terms.
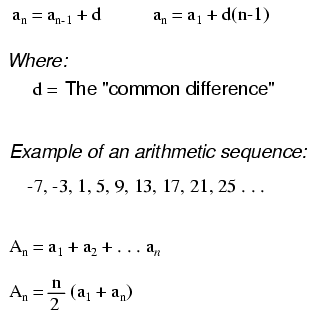
It is the progression where the last term is defined. Finite geometric progressionįinite geometric progression contains a finite number of terms. Let us see the information about each of these. The geometric progression is of two types. To find the terms of a geometric series, we only need the first term and the constant ratio. The common ratio can have both negative as well as positive values. where 'a' is the first term and 'r' is the common ratio of the progression. The GP is generally represented in form a, ar, ar 2. A geometric progression is a special type of progression where the successive terms bear a constant ratio known as a common ratio.


 0 kommentar(er)
0 kommentar(er)
